>【理論】平成21年 問5|複数のコンデンサ回路における電界のエネルギー比較に関する計算問題
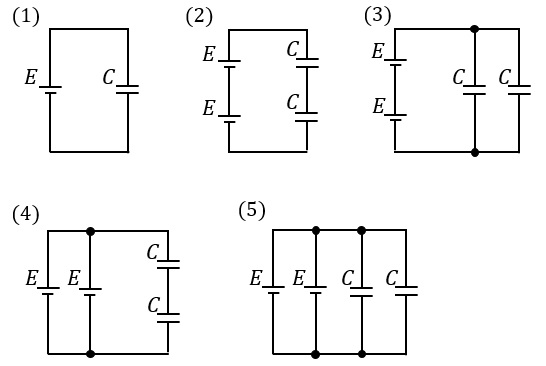
図に示す \( 5 \) 種類の回路は,直流電圧 \( E \) [V] の電源と,静電容量 \( C \) [F] のコンデンサの個数と組み合わせを異にしたものである。
これらの回路のうちで,コンデンサ全体に蓄えられている電界のエネルギーが最も小さい回路を示す図として,正しいのは次のうちどれか。
合格への方程式
コンデンサの合成静電容量
コンデンサは電気回路において電荷を蓄える素子で、その性質は静電容量(単位:ファラド[F])で表されます。複数のコンデンサを組み合わせると、回路全体としての合成静電容量を計算する必要があります。
コンデンサ容量が\( C_{1} \mathrm{[F]} \)と\( C_{2} \mathrm{[F]} \)のコンデンサがある場合、直並列の合成静電容量\( C \mathrm{[F]} \)は下記の通りとなります。抵抗の場合と直並列が逆になることを知っておきましょう。
①並列回路の合成静電容量
\[ \begin{aligned} C &= C_{1} + C_{2} \\[10pt] \end{aligned} \]
②直列回路の合成静電容量
\[ \begin{aligned} \frac{1}{C} &= \frac{1}{C_{1}} + \frac{1}{C_{2}} \\[10pt] \end{aligned} \]
整理すると、
\[ \begin{aligned} C &= \frac{C_{1}C_{2}}{C_{1}+C_{2}} \\[10pt] \end{aligned} \]
例題1
静電容量\(6 \mu \mathrm{F}\)と\(3 \mu \mathrm{F}\)のコンデンサを直列接続した場合の合成静電容量を求めなさい。
解答
\(C = \frac{C_{1}C_{2}}{C_{1}+C_{2}} = \frac{6 \times 3}{6 + 3} = \frac{18}{9} = 2 \mu \mathrm{F}\)
直列接続では常に合成静電容量は個々のコンデンサの静電容量よりも小さくなります。これは直列接続によって電気力線の通り道が狭くなるイメージです。
例題2
静電容量\(4 \mu \mathrm{F}\)と\(8 \mu \mathrm{F}\)のコンデンサを並列接続した場合の合成静電容量を求めなさい。
解答
\(C = C_{1} + C_{2} = 4 + 8 = 12 \mu \mathrm{F}\)
並列接続では合成静電容量は個々のコンデンサの静電容量の和になります。これは並列接続によって電荷を蓄える面積が増えるイメージです。
| 接続方法 | コンデンサの合成静電容量 | 抵抗の合成抵抗 |
|---|---|---|
| 並列接続 | \(C = C_{1} + C_{2}\) | \(\frac{1}{R} = \frac{1}{R_{1}} + \frac{1}{R_{2}}\) |
| 直列接続 | \(\frac{1}{C} = \frac{1}{C_{1}} + \frac{1}{C_{2}}\) | \(R = R_{1} + R_{2}\) |
コンデンサの静電エネルギー
コンデンサは電荷を蓄えることでエネルギーを保存することができます。このエネルギーは「静電エネルギー」と呼ばれ、電荷と電圧の関係から計算することができます。この性質により、コンデンサはエネルギー貯蔵素子として様々な電子機器に応用されています。
コンデンサの静電エネルギー\( W \mathrm{[J]} \)は、コンデンサの静電容量\( C \mathrm{[F]} \)及びコンデンサにかかる電圧\( V \mathrm{[V]} \)とすると以下の式で表されます。
\[ \begin{aligned} W &= \frac{1}{2}CV^{2} \\[10pt] \end{aligned} \]
また、\( Q = CV \)の関係から、次の式も成り立ちます。
\[ \begin{aligned} W &= \frac{1}{2}QV \\[10pt] &= \frac{Q^{2}}{2C} \\[10pt] \end{aligned} \]
例題
静電容量\(4 \mu \mathrm{F}\)のコンデンサに\(12 \mathrm{V}\)の電圧をかけたとき、このコンデンサに蓄えられる静電エネルギーを求めなさい。
解答
\[ \begin{aligned} W &= \frac{1}{2}CV^{2} \\ \\[10pt] &= \frac{1}{2} \times 4 \times 10^{-6} \times 12^{2} \\ \\[10pt] &= 2.88 \times 10^{-4} \, \mathrm{J} \end{aligned} \]
- カメラのフラッシュ:コンデンサに蓄えた静電エネルギーを一気に放出
- 除細動器:心臓の状態を正常に戻すための電気ショック
- 電気自動車の回生ブレーキ:運動エネルギーを電気エネルギーとして回収
発展例題:RC直列回路の時定数
静電容量\(C\)のコンデンサと抵抗\(R\)を直列に接続したRC回路では、コンデンサの充電や放電は指数関数的に変化します。この回路の時定数\(\tau\)は以下の式で表されます。
\[ \begin{aligned} \tau &= RC \\[10pt] \end{aligned} \]
時定数\(\tau\)は、コンデンサの電圧が最終値の約63%(正確には\(1-e^{-1} \approx 0.632\))まで変化するのに要する時間です。充電または放電が始まってから時間\(t\)における電圧\(V(t)\)は次式で表されます。
充電時:\(V(t) = V_0(1-e^{-t/\tau})\)
放電時:\(V(t) = V_0e^{-t/\tau}\)
ここで\(V_0\)は初期電圧または最終電圧です。
🔍 ワンポイントアドバイス: コンデンサの合成静電容量は抵抗とは逆の法則になることを覚えておきましょう。直列と並列の公式を混同しないように、「コンデンサは並列で足し算、直列で分数」というように覚えると良いでしょう。また、静電エネルギーの公式は蓄電池や発電機など、他のエネルギー変換システムを理解する際にも役立ちます。特に\(W = \frac{1}{2}CV^2\)の公式は、電気エネルギーの基本的な式として電子工学の様々な分野で登場します。実際の電子回路設計では、コンデンサの漏れ電流や等価直列抵抗(ESR)なども考慮する必要があります。
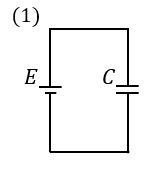
(1)の選択肢は、コンデンサが1個だけ直列に接続された回路やな!
このとき、電源電圧 \( E \) がそのままコンデンサにかかるから、
蓄えられるエネルギー \( W_1 \) は次の式で計算できるんやで。
\[ W_1 = \frac{1}{2} C E^2 \]
この式、覚えてるかな?コンデンサに蓄えられるエネルギーの公式や!
はい、先生! \[ W_1 = \frac{1}{2} C E^2 \] で求められますね。
これはよく出る公式なので、ちゃんと覚えておきます!
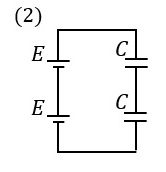
(2)の選択肢は、同じ容量のコンデンサが2個、**直列**につながってる回路やで!
直列つなぎのときは、合成静電容量はこうなるんやったな:
\[ C_{\text{eq}} = \frac{C \cdot C}{C + C} = \frac{C}{2} \]
さらに、電源電圧は \( 2E \) [V] かかっとるから、
エネルギーはこの式で出せるで!
\[ W_2 = \frac{1}{2} \cdot \frac{C}{2} \cdot (2E)^2 \]
この式、展開してみよか!
はい、先生!まずは \((2E)^2 = 4E^2\) ですね!
それを代入して式を整理すると:
\[ W_2 = \frac{1}{2} \cdot \frac{C}{2} \cdot 4E^2 = \frac{4CE^2}{4} = CE^2 \]
なので、 \( W_2 = CE^2 \ \mathrm{[J]} \) です!
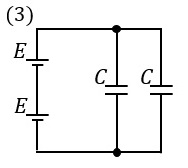
(3)の選択肢は、コンデンサが2個**並列**につながってる回路やな!
並列つなぎやと、合成静電容量は足し算になるから、
\[ C_{\text{eq}} = C + C = 2C \]
ほんで、この回路には電源電圧 \( 2E \) [V] が加わっとる。
ということは、エネルギーはこの式になるで!
\[ W_3 = \frac{1}{2} \cdot 2C \cdot (2E)^2 \]
この式、計算してみよか!
はい、先生!まず \((2E)^2 = 4E^2\) を使って式を展開すると、
\[ W_3 = \frac{1}{2} \cdot 2C \cdot 4E^2 \]
次に、係数をかけ算すると:
\[ W_3 = 4CE^2 \]
ということで、 \( W_3 = 4CE^2 \ \mathrm{[J]} \) になります!
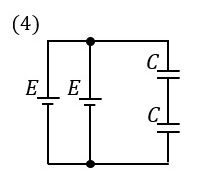
(4)の選択肢は、コンデンサ2個が**直列**につながってて、電源電圧は \( E \) [V] や!
直列のときの合成容量、覚えてるか?こうやったな:
\[ C_{\text{eq}} = \frac{C \cdot C}{C + C} = \frac{C}{2} \]
電圧は \( E \) そのままかかるから、エネルギーの式はこうなる!
\[ W_4 = \frac{1}{2} \cdot \frac{C}{2} \cdot E^2 \]
さあ、この式を整理していこか!
はい、先生!分数の掛け算から順に計算しますね。
\[ W_4 = \frac{1}{2} \cdot \frac{C}{2} = \frac{C}{4} \]
それに \( E^2 \) をかけて、
\[ W_4 = \frac{C}{4} \cdot E^2 = \frac{1}{4}CE^2 \]
ということで、 \( W_4 = \frac{1}{4}CE^2 \ \mathrm{[J]} \) になります!
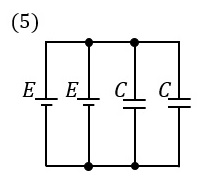
(5)の選択肢は、コンデンサが2個**並列**につながってて、それぞれに**電圧 \( E \) [V]** がかかってる回路やで!
並列のときの合成静電容量はこうやったな:
\[ C_{\text{eq}} = C + C = 2C \]
そんで、電圧は \( E \) がそのまま全体にかかってるから、
エネルギーの式はこうなるで!
\[ W_5 = \frac{1}{2} \cdot 2C \cdot E^2 \]
この式を整理して、最終的なエネルギー求めてみよか!
はい、先生!まずは係数の部分を計算してみます。
\[ \frac{1}{2} \cdot 2C = C \]
これに電圧の二乗 \( E^2 \) をかけると、
\[ W_5 = C \cdot E^2 = CE^2 \]
ということで、 \( W_5 = CE^2 \ \mathrm{[J]} \) になります!
ここまでで (1) 〜 (5) のそれぞれのエネルギーを求めたけど、
さいごに「どの回路が一番エネルギー少ないか?」を比べてみよか!
まず、それぞれのエネルギーをもう一度書き出してみるで:
(1) \( W_1 = \frac{1}{2} C E^2 \)
(2) \( W_2 = CE^2 \)
(3) \( W_3 = 4CE^2 \)
(4) \( W_4 = \frac{1}{4}CE^2 \)
(5) \( W_5 = CE^2 \)
この中で、一番小さい値になってるんはどれやと思う?
はい、先生!それぞれ比べてみると…
(1) は \( \frac{1}{2}CE^2 \)
(2) と (5) は \( CE^2 \)
(3) は \( 4CE^2 \)
(4) は \( \frac{1}{4}CE^2 \)
なので、一番小さいのは
\[ W_4 = \frac{1}{4}CE^2 \]
つまり、エネルギーが最も小さいのは(4)の回路ですね!
解説まとめ
(1) コンデンサに蓄えられるエネルギー \( W_1 \) [J] は、次の式で求められます:
\( W_1 = \frac{1}{2}CE^{2} \ \mathrm{[J]} \)
(2) コンデンサの合成静電容量は、
\( \frac{C \cdot C}{C + C} = \frac{C}{2} \ \mathrm{[F]} \)
したがって、コンデンサに蓄えられるエネルギー \( W_2 \) は、
\( W_2 = \frac{1}{2} \cdot \frac{C}{2} \cdot (2E)^2 \)
\( = CE^{2} \ \mathrm{[J]} \)
(3) コンデンサの合成静電容量は、
\( C + C = 2C \ \mathrm{[F]} \)
したがって、コンデンサに蓄えられるエネルギー \( W_3 \) は、
\( W_3 = \frac{1}{2} \cdot 2C \cdot (2E)^2 \)
\( = 4CE^{2} \ \mathrm{[J]} \)
(4) 合成静電容量は、
\( \frac{C \cdot C}{C + C} = \frac{C}{2} \ \mathrm{[F]} \)
全体に加わる電圧が \( E \ \mathrm{[V]} \) であるとすると、エネルギー \( W_4 \) は、
\( W_4 = \frac{1}{2} \cdot \frac{C}{2} \cdot E^{2} \)
\( = \frac{1}{4}CE^{2} \ \mathrm{[J]} \)
(5) 合成静電容量は、
\( C + C = 2C \ \mathrm{[F]} \)
それぞれのコンデンサに加わる電圧が \( E \ \mathrm{[V]} \) であるとすると、エネルギー \( W_5 \) は、
\( W_5 = \frac{1}{2} \cdot 2C \cdot E^{2} \)
\( = CE^{2} \ \mathrm{[J]} \)
以上から、蓄えられるエネルギーが最も小さいのは (4) であることが分かります。